Geniitwo's World

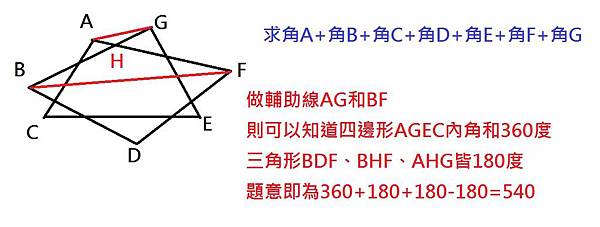
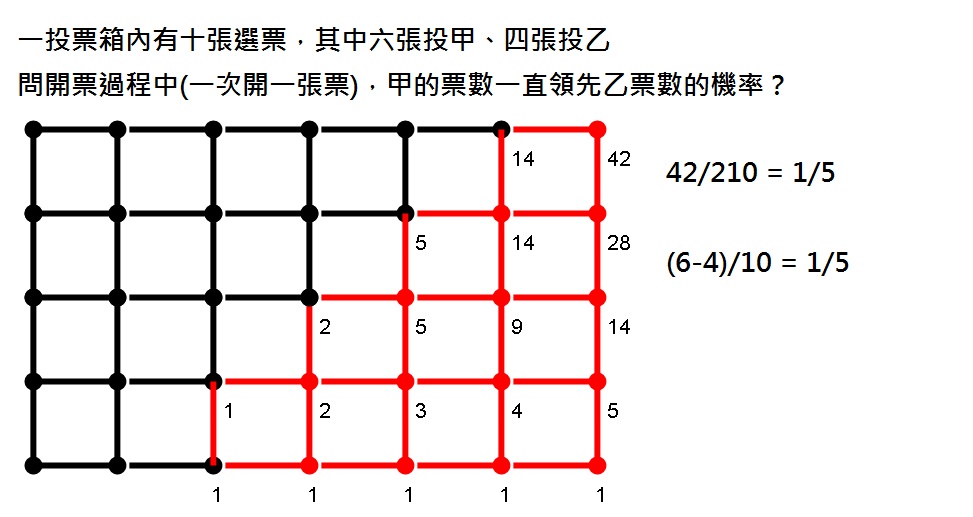
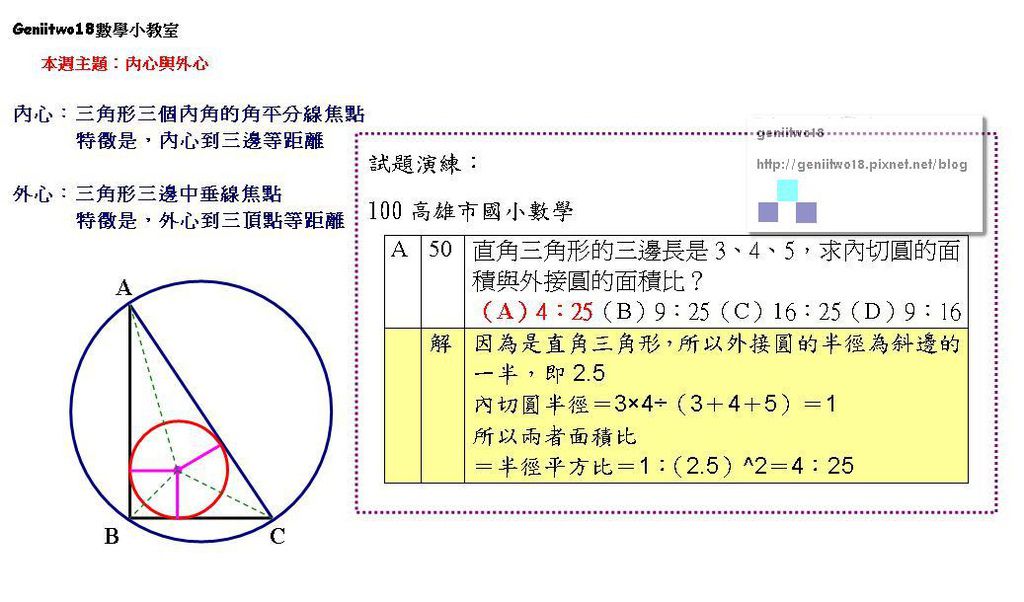
1

有一堆相同的長方體盒子，每個盒子的長是18公分、寬是15公分、高是10公分；問最少需要(270)個長方體盒子，才能拼成一正方體。

[18,15,10]=90 所以是5x6x9=270

2.

若x=1+√3，則x^2-4=(   2√3　　)。

x=1+√3，則 x^2= 4+2√3

則本題答案是2√3

3

若x+2 是x^2-3x+2+a 的因式，則a=(-12)。

將x=-2帶入 4+6+2+a=0  則a=-12

4

班上30位同學的數學成績由小到大依序分成低分組、中分組和高分組各10人。若   全班平均70分、高分組平均85分、中分組平均75分，則低分組的平均成績(50)分。

(70x30-85x10-75x10)/10 = 210-85-75 = 50

5

若將正整數從1開始依序排列，其規律如下表：

第1列　1

第2列　2　3

第3列　4　5　6

第4列　7　8　9　10

則第100列最後一個數是(5050)。

(1+100)x100/2 = 5050

6

環保人士推動消毒水的製作方式如下：

將橘皮放入95%濃度的酒精中，浸泡後再用煮沸後的冷開水稀釋成70%~75%的酒精濃度，有最佳的消毒效果。

若有0.6公升的95%濃度的酒精，放入橘皮浸泡(其釋出的成份可不計)後，想要達到上述最佳消毒效果的酒精濃度；問最少和最多需加入多少毫公升的冷開水？(答案請四捨五入取至個位) 214毫公升

0.6公升=600毫公升

600*0.95=570(純酒精)

570/0.7 = 約814 

570/0.75=760 

所以本題答案是814-600=214和160

7

四邊形ABCD中，且，如下圖。若長為整數，則長的所有可能值為何？BD=7,8,9

根據兩邊和大於第三邊，可知BD<5+6=11   BD<10+4=14

根據兩邊差小於第三邊，可知BD>1  BD>6

取所有條件交集，知道6<BD<11  所以BD=7,8,9,10

8

請針對「加乘混合」兩步驟問題，設計以下兩種不同文字題，並寫出該問題的併式紀錄：(1)先加後乘。【2.5分】(2)先乘後加。【2.5分】

(1)小傑每個月存100元，奇犽每個月存75元。六個月後兩人共存幾元？

    (100+75)x6x=175x6=1050

(2)雷歐力買了10元的巧克力3條和1杯45元的咖啡，共花了多少錢？

    10x3+45 = 75

9

學生使用量角器測量角度及報讀角度時，常發生錯誤。請分別針對以下兩類活動，各舉出一項學生常見的錯誤及其原因：(1)測量角度。【2.5分】(2)報讀角度。【2.5分】

(1)未對齊0刻度：因為學生對量角器上的結構

(2)將110度報讀成70度；因為學生對鈍角、銳角與直角關係尚不清楚

10

某生進行「」直式計算時，某生列出的直式作法如下：

              (1)請指出該生可能的迷思概念為何？【2分】

                (2)請寫出針對該生的補救教學重點為何？【3分】

(1)不知道位值概念，也就是教學現場常會說的小數點對齊，只記得靠右對齊

(2)為了加強他的位值概念，可使用定位板，讓他知道0.5的5是十分位數，而10.73的3是百分位數

11

老師出了兩個有關角柱的試題如下：

甲題：「一個五角柱，它有幾個面？① 5  ② 6  ③ 7  ④ 8」

乙題：「一個角柱有7個面，它是什麼形體？

①三角柱  ②四角柱  ③五角柱  ④六角柱」

請比較這兩試題的難度，並說明理由。

甲題較乙題容易

因為在角柱單元的認識上，是透過許多不同個別形體的角柱，如三角柱、四角柱、五角柱、六角柱、圓柱，來統整歸納角柱的特性。

所以若以五角柱來出題，顯然是個殊性較高，學生容易作答；反之，乙題的角柱一詞已屬於統整性的概念，所以學生不易作答。

①

46

利用除法運算可以將有理數化成小數，例如：1/2=0.5
即為有限小數，但1/3=0.3333…則不為有限小數。

甲：有理數分母的因數必包括2 或5，則此有理數為有限小數。

乙：有理數分母的因數分解後，其因數只包括 2 或5，則此有理數為有限小數 

丙：有理數的分子必為 2 或5 的倍數，則此有理數為有限小數

丁：有理數分子的因數分解後，其因數只包括2 或5，則此有理數為有限小數

關於有理數為有限小數的敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

正確的只有乙的敘述，其他三個皆可舉出反例

甲：有理數分母的因數【未必】包括2或5，也能是有限小數，例：3/3

丙：有理數的分子【未必】為2或5的倍數，也能是有限小數，例：3/10

丁：2/3的分子因數分解後只有2，但並非有限小數

③

47

能力指標用於表示不同能力的種類與難易，就有理數的教學而言，被除數與除數均為有理數時仍屬小學的數學教材範圍，關於有理數教學教材的四個敘述，

甲：被除數與除數均為整數。       乙：被除數與除數均為有理數。

丙：被除數為有理數與除數為整數。 丁：被除數為整數與除數為有理數。

簡單到困難的教學順序？

①甲乙丙丁  ②甲丁丙乙 
③甲丙丁乙  ④甲丁乙丙。

解

整數÷整數 → 有理數÷整數
→ 整數÷有理數 → 有理數÷有理數

③

48

甲：規則無限循環小數必可化為有理數。

乙：無理數是不規則的無限小數。

丙：有限小數恆可表示為分母是10 的有理數。

丁：任何一個可以比大小的數一定是有理數。

關於數與量的敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

丁是錯的，π比1大，但是π是一個無理數

②

49

(5+7)+8=5+(7+8)是滿足

①交換律  ②結合律  ③分配律  ④遞移律。

解

前面結合和後面結合

③

50

甲：An 表n 之所有倍數之集合，m 是n 的因數(m＜n)，則An⊂Am 且An≠ Am 乙：Jn 表n 之所有因數之集合，m 是n的倍數(m＞n)，則Jn ⊂Jm 且Jn ≠ Jm

丙：n=36 時，Jn 共有9 個元素

丁：n=36
時，An 共有無限多個元素。關於因數與倍數的敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

丙是錯的，若n=36，Jn 表n之所有因數之集合，應該有18個元素（正負因數）

②

36

已知敘述p 為真，敘述q 為假，敘述r 為真，

甲：( p→q )∧ (q→r)。 乙：p→(q∨r)。 丙：q→∼r。 丁：p→q。

關於上述之甲、乙、丙、丁四個敘述，恆真的共有幾個？

①1  ②2  ③3  ④4。

解

恆真的是乙（T→T）和丙（F→T）

甲：F∧T（結果還是False），丁：T→F（結果還是False）

②

37

甲：由正三邊形組成的正多面體共有2 個。

乙：形成多面體的一個頂點至少要有3 個正多邊形拼在一起。

丙：正十二面體共有30 個頂點數。

丁：正二十面體共有30 個稜線數。

關於空間幾何形體甲、乙、丙、丁四個敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

乙和丁是對的

甲：正三角形組成的正多面體有【3】 個（正四面體、正八面體、正二十面體）

丙：正十二面體共有【30】個頂點數

②

38

數學家尤拉（Euler）發現空間上的幾何形體，均存在一個有趣的規則，關於尤拉數的正確敘述是

①尤拉數指幾何圖體的面數＋幾何圖體的頂點數－幾何圖體的稜線數=1

②尤拉數指幾何圖體的面數＋幾何圖體的頂點數－幾何圖體的稜線數=2。񗹤

③尤拉數指幾何圖體的面數＋幾何圖體的稜線數－幾何圖體的頂點數=2。

④尤拉數指幾何圖體的面數＋幾何圖體的稜線數－幾何圖體的頂點數=1。

解

這題如果沒有背，可以直接用正六面體（立方體）來推導

正四面體有6個面，8個頂點，12個邊，所以是：面＋頂點－邊＝2

②

39

甲：柱體的邊數必為偶數。       乙：錐體的邊數必為偶數。

丙：錐體的頂點數必為3 的倍數。 丁：柱體的頂點數必為偶數。

關於柱體與錐體的敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

正確的是乙和丁

甲：柱體的邊數【未必】是偶數，三角柱的邊數是9

丙：錐體的頂點數【未必】為3的倍數，四角錐的頂點數是5

②

40

甲：乘法對加法滿足分配律。

乙：滿足結合律的四則運算有乘法與加法。

丙：滿足交換律的四則運算有乘法與除法。

丁：除法對加法滿足分配律。

關於數的代數性質的敘述，正確的共有幾個？

①1  ②2  ③3  ④4。

解

數學上只討論加法和乘法兩種運算，常見的是

加法的交換律、結合律

乘法的交換律、結合律，以及乘法對加法的分配律

因此這一題敘述正確的是甲和乙

②

06

設一組15個數的平均數為m，若從此組數中抽走0、2、10，餘下12個數的平均數為m+ 2，則m =？

①10 ②12 ③14 ④16。

解 

原先的平均數是m，所以總和是15m，現在抽走0、2、10

總和變成15m─0─2─10＝15m－12

剩餘的數平均數是m＋2，所以總和表示成12（m＋2）

15 m－12＝12（m＋2）→ 3m = 36  m＝12

④

07

若a +8，a − 5， a + 2,，a −1，a +14的中位數為12，則這5個數的平均數為何？

①13.3  ②13.4  ③13.5  ④13.6。

解

重新排序成a－5，a－1，a＋2，a＋8，a＋14

因為中位數是12，所以a＋2＝12  因此a＝10

平均數＝（a－5＋a－1＋a＋2＋a＋8＋a＋14）/5＝（5a＋18）/5

＝68/5＝13.6

①

08

若二次方程式x2 + 4x
+ k =1沒有實根，則k取值的範圍為何？

①k > 5  ②k ≥ 5  ③k < 4  ④k ≤ 4。

解

方程式沒有實根，表示判別式D＝b^2－4ac＜0

所以4^2－4×1×（k-1）＜0

16－4（k-1）＜0 → k-1＞4   故k＞5

①

09

試求等比級數 5/2 ＋ 5/4 ＋
5/ 8+……的總和為何？

①5  ②−5  ③1/5  ④ -1/5

解

原式＝（5/2）×（1＋1/2＋1/4＋……）＝（5/2）×（1/(1-1/2)）＝5

②

10

設L 為一直線，若其斜率為log2 3，則與L 互相垂直之直線的斜率為何？

①  log3 2 ②−log3 2 ③  log2^-1 3  ④ − log2^-1 3

解

兩線互相垂直，表示兩線的斜率相乘等於-1

100中區聯招國小數學Q1~Q5

④

01

若e 是自然對數的底數，π 是圓周率，則下列哪個數最大？

①π  ②√10  ③3.15  ④9/ e 。

解 

π≒3.14  √10≒3.16 
e≒2.718  9/e≒3.31

①

02

若一實心圓錐體的底半徑減少30%且高增加60% ，則該圓錐體的體積改變為何？

①減少21.6%  ②減少30%  ③增加21.6%  ④增加30%。

解

圓錐體的體積與半徑平方×高成正比

所以此題圓錐體改變是：（0.7）^2×1.6＝0.784  減少了21.6％

③

03

在座標平面上若y = −x^2 − 4x + 2k的圖形與x軸相切，則k =？

①2  ②4  ③−2  ④−4。

解

圖形與x軸相切，表示y＝0

0＝-x^2－4x＋2k＝-（x^2＋4x＋4）＋4＋2k

＝-（x＋2）^2＋4＋2k

4＋2k＝0   故k＝-2

①

04

下列何者為三角形三個邊的垂直平分線的交點？

①外心  ②垂心  ③重心  ④內心。

解

重心：三個邊的中線交點

內心：三個角的角平分線交點

③

05

試求−6
< −3x +
4 <12 − x的解？

①x > 10/3  ②x < −4或x >10/3  ③ −4 < x <10/3  ④ x <10/3

解

-6＜-3x＋4＜12－x → -10＜-3x＜8－x

-10＜-3x → x＜10/3 ； -3x＜8－x → -2x＜ 8 
x＞-4

故 -4 ＜x＜10/3